The world around us is composed of systems, whether its solar system, digestive system, ecosystem or social system, they all have different entities, objects, or players that work together and share complex relationships with each other. Networks act as a general language for describing and modelling such complex systems. For instance let’s say we have 10 objects, they can be anything from people, phones or genes, we represent them as dots (or nodes).
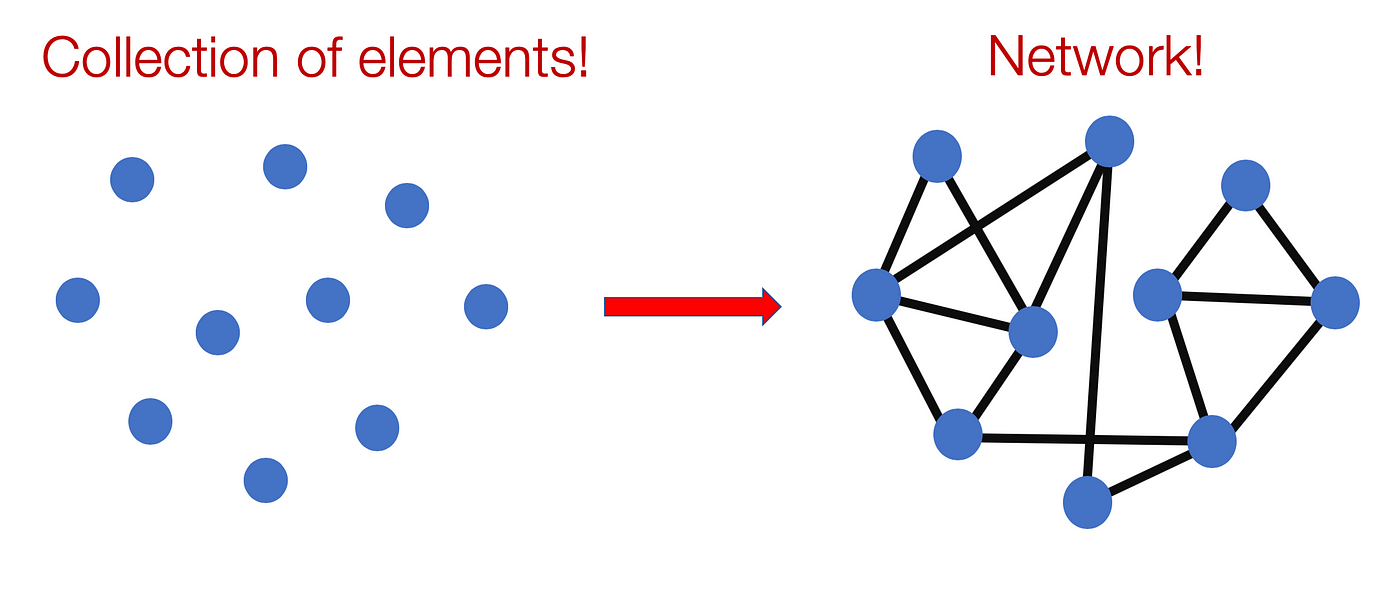
A simple network of interconnected elements
The lines (edges) between those dots show if they are connected to each other or not. So basically a network can be considered as a collection of elements whose property is determined by interconnectivity between them. Network science uses graph theory to model the properties of these connections to determine features such as the most important element in a network, what local communities exist within them and how does information flow across them. For each of these, data scientist employ graph theory and linear algebra to make their predictions.
There are three main ways in which networks can be analysed Node Classification, Link Prediction, and Community Detection. In this blog post I will just present a brief summary of what each of them are.
Ways To Analyse Networks
Node Classification:
Node classification aims to determine the label of nodes (sometimes called vertices) based on other labelled nodes and the topology of the network. They are usually a form of semi-supervised learning. Most often it is difficult or expensive to collect the true label for each node in our network, so oftentimes in real world setting we rely on random sampling to obtain these labels. We then use those random sample of labels to develop models that can be used to generate trustworthy node label predictions for our graph.
A good example of was provided in the following kdnuggets post, where we need to infer an online social network member’s music preferences.
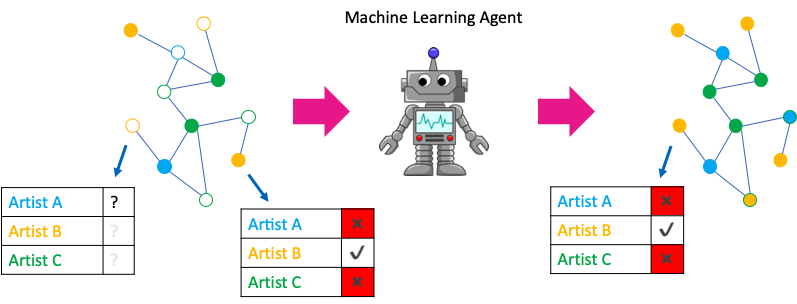
image taken from www.kdnuggets.com/2019/08/neighbours-machine-learning-graphs.html
Link Prediction:
Link prediction refers to the task of predicting missing links or links that are likely to occur in the future. Originally Link Prediction was used in the uncovering of terrorist networks, but nowadays it has been used in recommender system, predict spread of disease, etc. For example, let’s say we have a social network and we want to predict which nodes among them are likely to connect (friend recommendation in Facebook). Another example could be predicting which diseases a new drug might treat.
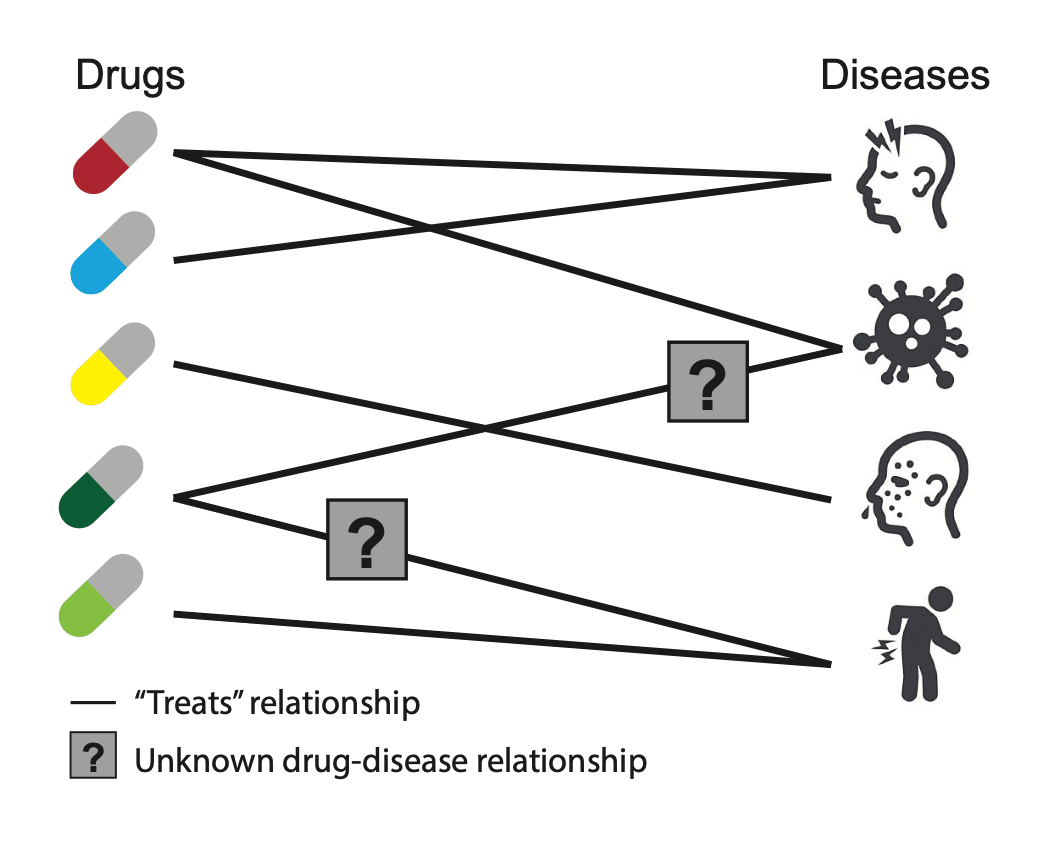
Image source: snap.stanford.edu/deepnetbio-ismb — ISMB 2018
Community Detection:
Clustering is used to find subsets of similar nodes and group them together. For example many websites that contain trojan/malware tend to link to each other. Detecting communities of such websites is extremely useful because the whole network can get exposed if even 1 rogue website it found. This is also the reason why many of these websites use Javascript redirects to link to each other (instead of typical ‘href’ links), so that they avoid detection by naive scraping algorithms.
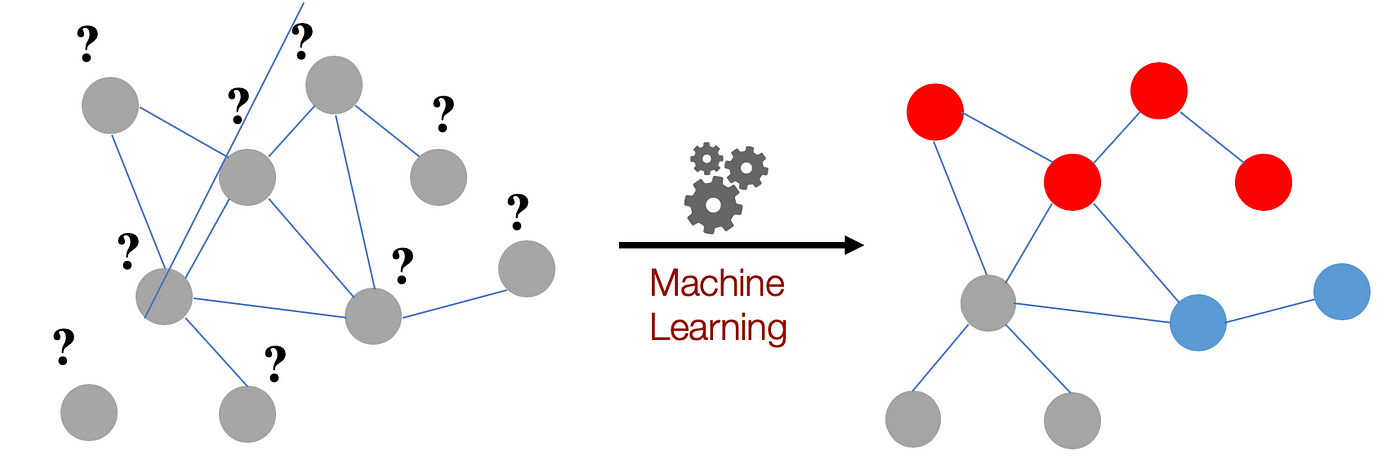
Clustering can help identify malware (red) sites from normal (blue) and help remove links between them
Sometimes while working with larger complex networks it’s helpful to first cluster users together in order to simplify the network and increase the efficacy of predictive models. This discussion (Does preclustering help to build a better predictive model?) provides a decent overview of why this is so.
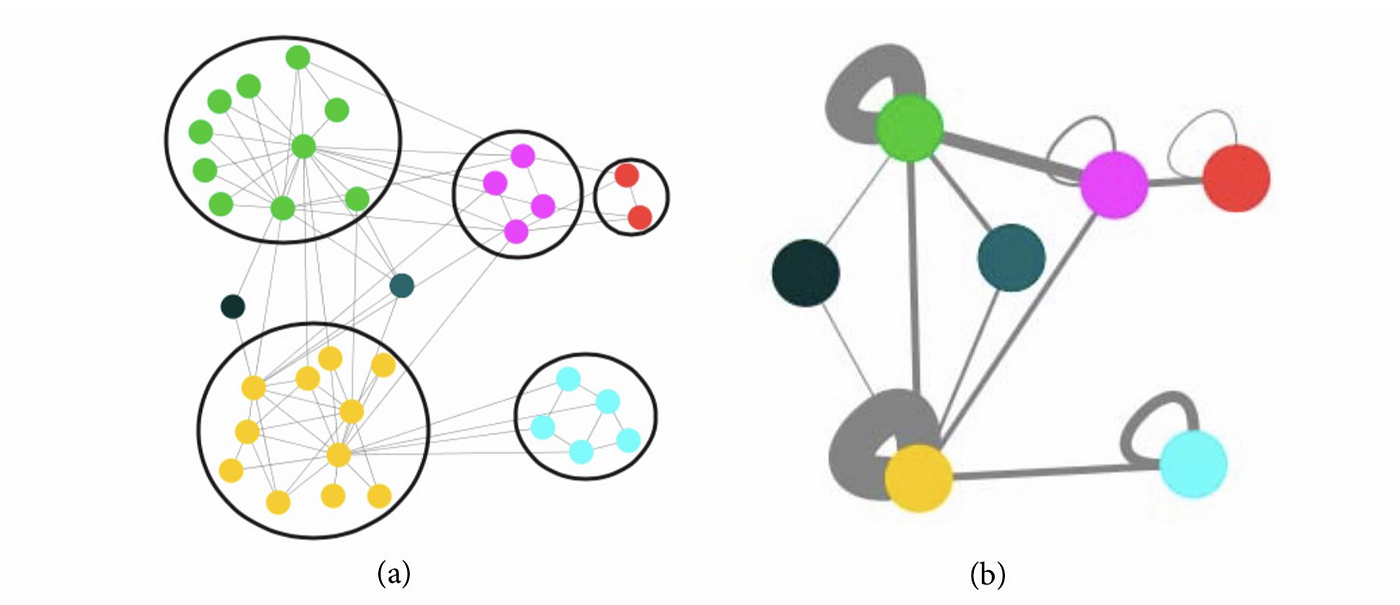
Image taken from arXiv:1909.10491
What Are Graph Embeddings?
Representing networks in the form of graphs makes it very intuitive for us to understand complex relationships but it can be very difficult to work with for a computer. Graphs contain edges and nodes, those network relationships can only use a specific subset of mathematics, statistics, and machine learning. Any machine learning model that aims to solve the graph-based problems (mentioned above) uses either the adjacency matrix of the graph or the vector spaces that are derived from the graph. Lately vector spaces have become popular.
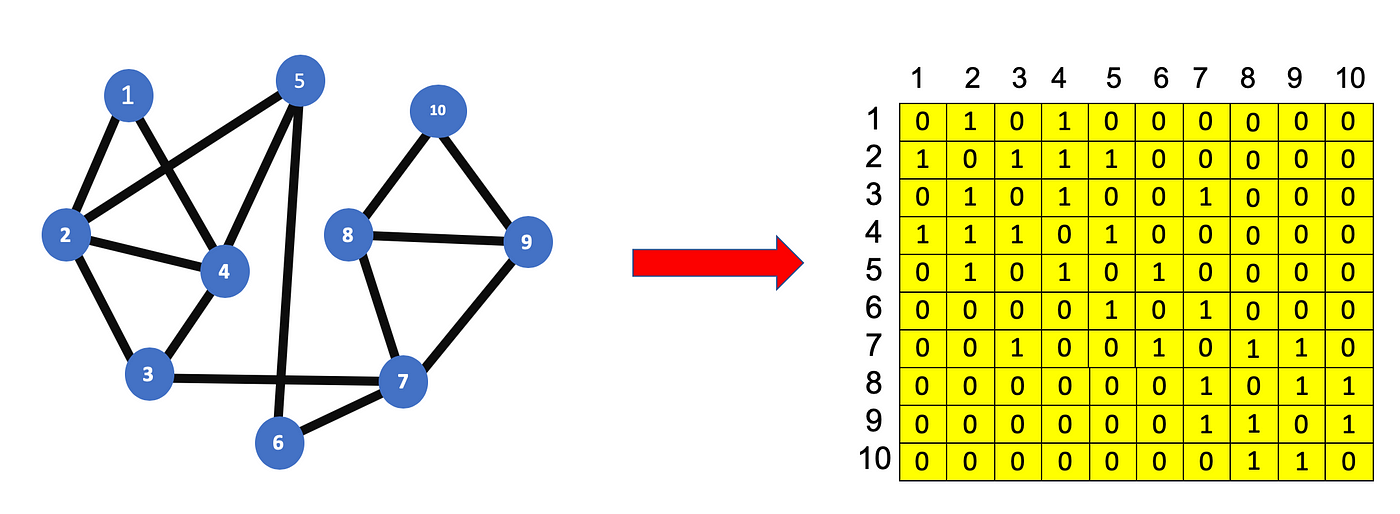
Adjacency matrix for our simple network
In our simple network consisting of just 10 nodes we get a 10*10 adjacency matrix, which is a numerical representation of which nodes are connected to each other. Most real world networks tend to be complex, so if a graph has a |V| * |V| adjacency matrix where |V| = 1M, then it’s hard to use or process a 1M * 1M numbers in an algorithm. This is where embeddings serve a useful purpose.
Graph embedding learns a mapping from a network to a vector space, while preserving relevant network properties. These embeds are “latent vector representation”, with dimension ‘d’, where d « |V|. This means we eventually get an adjacency matrix |V| * d which is relatively easier to use.
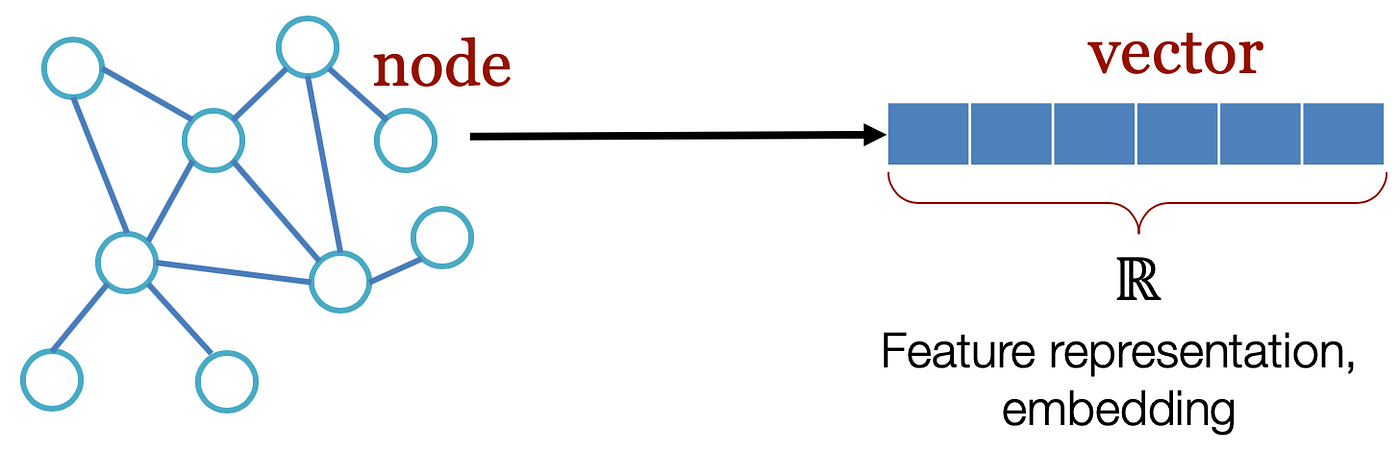
The term graph embeddings are used in two different ways:
Node Embeddings — Here we find a fixed length vector representation for every nodes in our graph (similar to word embeddings). We can then compare the different nodes by plotting these vectors in d d-dimensional space and interestingly “similar” vertices are plotted closer to each other than the ones which are dissimilar or less related.
Node embeddings are useful for node classification tasks. As an example we can consider a simple scenario where we want to recommend products to people who have similar interests in a Facebook. By getting node embeddings (here it means vector representation of each person), we can find the similar ones by plotting these vectors and this makes recommendation easy.
Graph Embeddings — Here we find the latent vector representation of the whole graph itself. They are useful for link prediction and community detection tasks. For example, if we have a group of chemical compounds for which you want to check which compounds are similar to each other, how many type of compounds are there in the group (clusters) etc. We can use these graph embedding vectors and plot them in space to answer those questions.
References:
- snap.stanford.edu/deepnetbio-ismb — ISMB 2018
- arXiv:1909.10491
- arXiv:1705.02801
- www.kdnuggets.com/2019/08/neighbours-machine-learning-graphs.htm