One of the key points of Graph Theory is that it conveys an understanding of how things are interconnected via nodes (points where various paths meet) or edges (the paths connecting the nodes). There are a number of different types of graphs, of which the most well-known are digraphs (directed graphs, whereby A may lead to B, but the reverse may not be true), an undirected graphs (where there is no implied directionality). One of it major application is in trying to understand networks, and when graph theory is applied to complex networks the insights they reveal may seem more magic than math. For instance, Facebook (and almost all other social networks) model the users and their connections with their friends in a graph structure. And, they use this graph model to do their business by applying graph theory ideas to learn more about how to populate your timeline, what advertisements to show, etc. Google, uses a graph representation to store/retrieve the semantic relationship between different entities, which they call it, Knowledge Graph, as well as providing you with the top relevant webpages for your query, using PageRank algorithm, which is a graph theoretic algorithm.
A fairly common feature of complex networks is that they consist of sets of nodes that interact more with one another than with nodes outside the set. Social networks, for instance, might consist of tightly knit communities of friends with rarer friendship ties between different communities. In protein interaction networks, certain groups of proteins interact with one another more frequently than they do with proteins in other groups. If you map out a network of projects going on in a large company, certain projects will likely have more conceptual overlap and mutual dependency than others; this network structure will hopefully be mirrored to some degree by the organisational structure within the company.
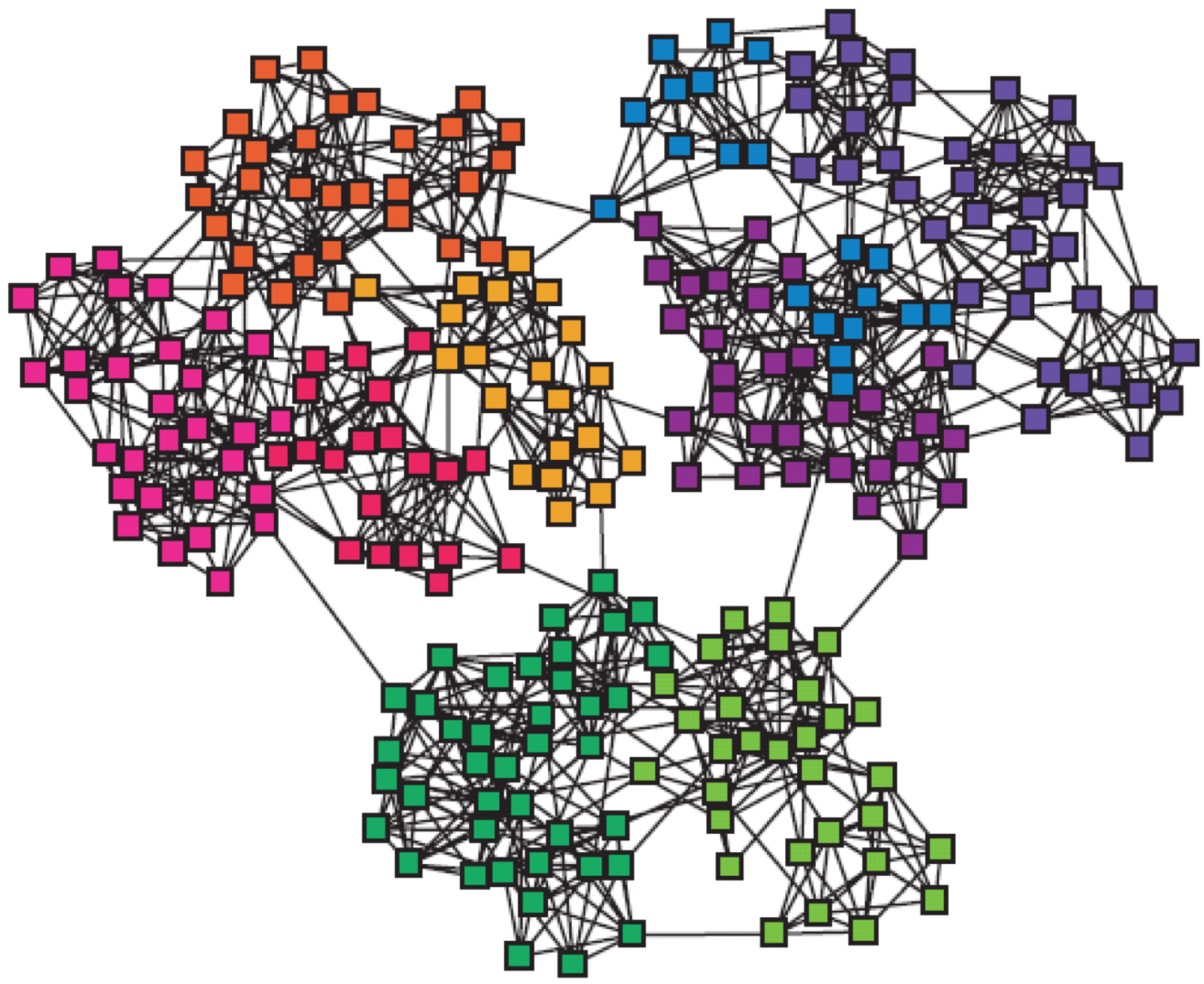
Communities emerge in a network because not all nodes are equally important, some nodes have greater“influence” over others compared to the rest, or are more easily accessible to other, or act as a go-between in most node-to-node communications. Finding out the most important node in a network is part of centrality analysis and the most commonly used measures are:
- Degree centrality
- Closeness centrality
- Betweenness centrality
Degree Centrality:
The more neighbours a given node has, the greater is its influence. In human society, a person with a large number of friends is believed to be in a favourable position compared to persons with fewer. Such a person can act as an influencer and they play important role within a social network. This leads to the idea of degree centrality, which refers to the degree of a given node in the graph representing a social network. The larger the degree the more important the node is and only a small number of nodes have high degree in real life networks.
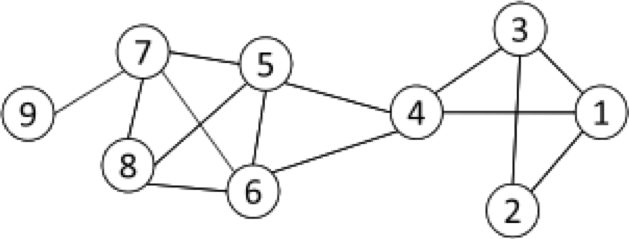
In the following example node 1 has a degree centrality of 3
Closeness centrality:
Nodes that are able to reach other nodes via short paths, or who are “more reachable” by other nodes via shorter paths, are in more favoured positions. Such nodes are “central” to the network as they can reach the whole network more quickly than non-central nodes. This structural advantage can be translated into power, and it leads to the notion of closeness centrality. It is the average distance from a given starting node to all other nodes in the network.
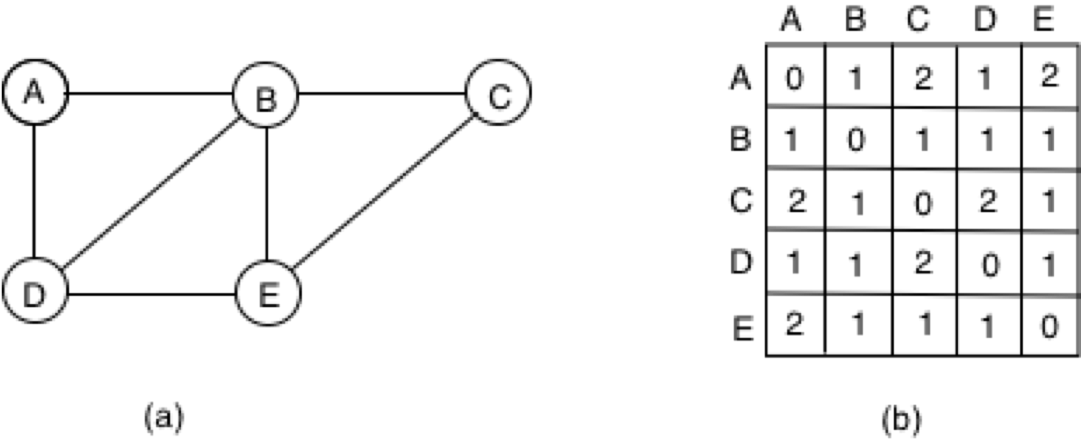
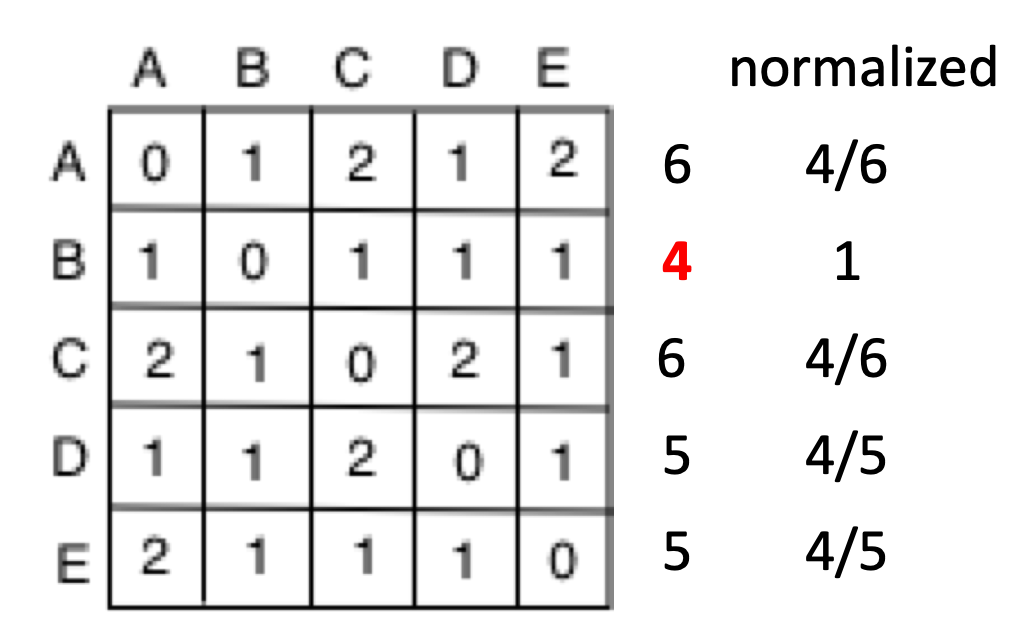
The path between nodes can be represented in the form of an adjacency matrix. In the figure we can reach from A to B and from A to D with just a single edge and so they have value of 1, but the distance from A to C and A to E is 2 as there are two edges between those nodes. When we add the overall distance that is needed to be traversed to reach all the nodes we get a value of 6 (0+1+2+1+2). There are 5 nodes in this network and not counting A we can find that on average the centrality of A is 4/6. We can do the following for all the nodes in the network and see that B has the highest closeness centrality of 1.
Betweenness Centrality:
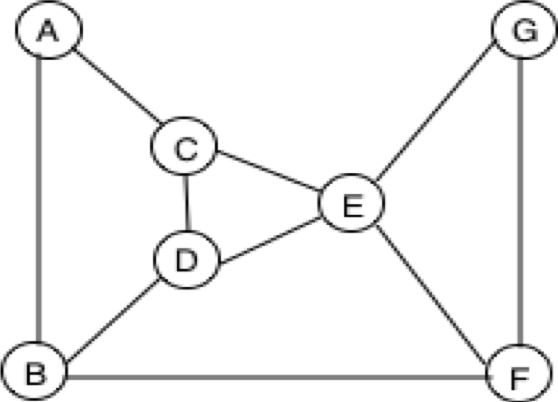
For each pair of nodes in a social network, consider one of the shortest paths- all nodes in this path are intermediaries. The node that belongs to the shortest paths between the maximum number of such communications, is a special node — it is a potential deal maker and is in a special position since most other nodes have to channel their communications through it. Such a node has a high betweenness centrality.
From each source node u to each destination node v, push 1 unit of flow via the shortest paths. If there are multiple shortest paths, then the flow will be evenly split. The amount of flow handled by a node or an edge is a measure of its betweenness centrality.

Betweenness centrality of C with respect to (A,G)
If each node sends 1 unit of flow to every other node (excluding C), then C will handle only 2. (1+ 1/2 + 1/2) = 4 units of flow.